Learning Preconditioners for Conjugate Gradient PDE Solvers
Publication
ICML 2023
Authors
Yichen Li, Peter Yichen Chen, Tao Du, Wojciech Matusik
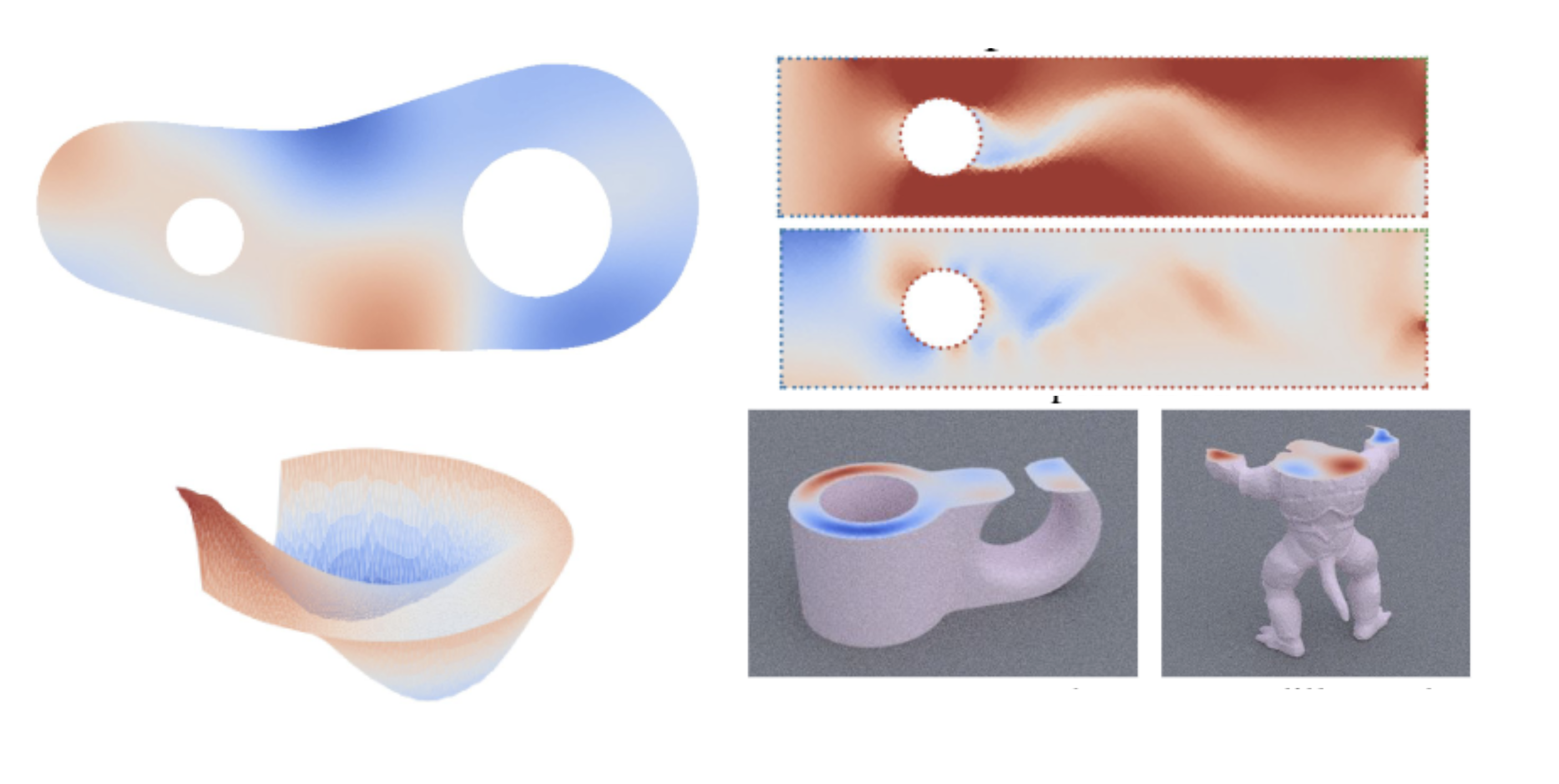
Abstract
Efficient numerical solvers for partial differential equations empower science and engineering. One commonly employed numerical solver is the preconditioned conjugate gradient (PCG) algo- rithm, whose performance is largely affected by the preconditioner quality. However, designing high-performing preconditioner with traditional numerical methods is highly non-trivial, often re- quiring problem-specific knowledge and meticu- lous matrix operations. We present a new method that leverages learning-based approach to obtain an approximate matrix factorization to the sys- tem matrix to be used as a preconditioner in the context of PCG solvers. Our high-level intuition comes from the shared property between precon- ditioners and network-based PDE solvers that ex- cels at obtaining approximate solutions at a low computational cost. Such observation motivates us to represent preconditioners as graph neural networks (GNNs). In addition, we propose a new loss function that rewrites traditional pre- conditioner metrics to incorporate inductive bias from PDE data distributions, enabling effective training of high-performing preconditioners. We conduct extensive experiments to demonstrate the efficacy and generalizability of our proposed approach on solving various 2D and 3D linear second-order PDEs.1